Einfluss der Radkörperstegbreite auf die Breitenlastverteilung
Bild: © FVA GmbHDas Ziel, die Leistungsdichte eines Getriebes zu erhöhen, setzt voraus, dass überschüssige Materialreserven erkannt und auf das notwendige Maß reduziert werden können. Dabei ist es wichtig, die Einflüsse auf das Getriebe zu kennen und welche Belastungen sich daraus ergeben. Am Beispiel eines zweistufigen Reduktorgetriebes, wie es in der Elektromobilität zum Einsatz kommt, wird der Einfluss der Radkörpergestaltung auf die Breitenlastverteilung und die dafür notwendige Korrektur dargestellt. Des Weiteren wird der Einfluss auf die lokale Last- und Pressungsverteilung analysiert.
Verschiedene Radkörperberechnungen in der FVA-Workbench
In der FVA-Workbench werden zwei verschiedene Möglichkeiten angeboten, wie ein Radkörper berechnet werden kann.
1. Option: Der Zahnkontakt wird über einen Finite-Elemente-basierten Ansatz gelöst. Innerhalb einer FE-Berechnung lassen sich komplexe Geometrien, wie z.B. ein beliebig geformter Radkörper, problemlos integrieren. Die Methode wurde im Forschungsprojekt FVA 484 V/VI entwickelt und verifiziert. Dabei wird der Einfach- und Mehrfacheingriff realitätsgetreu abgebildet.
2. Option: Der Radkörper wird über eine reduzierte Steifigkeitsmatrix in das Gesamtsystem integriert. In diesem Fall wird die Verzahnung nur über die Breite aufgelöst und an den Radkörper angebunden. Die Lösung der Verformungen inklusive der Berechnung der Breitenlastverteilung findet im Welle-Lager-Zahnrad-System statt.
Positionierung des CAD-Radköpers und Vernetzung
Die importierte CAD-Geometrie des Radkörpers wird im ersten Schritt korrekt positioniert, um die Anbindung an die Verzahnung zu ermöglichen. Der Aufwand für den Nutzer ist durch die Unterstützung mittels 3D-Ansicht und des Positionierungswizards sehr gering und macht das Konstruktionskoordinatensystem unabhängig von der Berechnung. CAD-Geometrien können einfach wiederverwendet und in viele verschiedene Getriebemodelle integriert werden.
Mit der leistungsstarken internen FE-Vernetzung in der FVA-Workbench können selbst komplexe Geometrien vernetzt werden. Neben linearen und quadratischen Elementen erlaubt der Vernetzer eine Bauteilvereinfachung indem automatisiert kleine, irrelevante Bohrungen entfernt werden können. Hierdurch kann die Netzgüte erhöht und gleichzeitig die Zahl der Elemente reduziert werden, was sich letztlich in einer erhöhten Berechnungsperformance widerspiegelt.
Berechnung der Steifigkeit
An der Kontaktfläche zwischen der analytischen Verzahnung und dem FE-Radkörper sowie an der Kontaktfläche zwischen Welle und Radkörper werden die FE-Anbindeknoten automatisiert identifiziert und farblich in der 3D-Ansicht markiert, sodass eine einfache Überprüfung durch die Ingenieurin oder den Ingenieur möglich ist. Die FE-Anbindeknoten sind notwendig um eine korrekte reduzierte Steifigkeitsmatrix FVA-Workbench-intern ermitteln zu können. Im Rahmen der Gesamtsystemberechnung wird nun anstelle eines einfachen Vollscheibenmodells für den Radkörper die realitätsgetreue Steifigkeitsmatrix verwendet.
Anwenderinnen und Anwender, die sich bereits intensiver mit der Berechnung von FE-Bauteilen beschäftigt haben, werden feststellen, dass die Wahl der Randbedingungen und die Vernetzung einen sehr großen Einfluss auf die Berechnung haben. Das beschriebene One-Click FEM-Verfahren stellt sicher, dass auch ohne spezielle FE-Kenntnisse zuverlässige und reproduzierbare Ergebnisse erzielt werden können.
Einfache Modelle – Vergleich mit einem FE-Vollscheibenrad
In einem ersten Versuch soll das Standardmodell der FVA-Workbench, ein Vollscheibenrad, mit einem FE-Radkörper nachgerechnet werden. Als Beispiel wird ein Reduktorgetriebe verwendet, wie es häufig für Elektroantriebe in PKWs eingesetzt wird. Die Verzahnung ist so ausgelegt, dass bei einer Antriebsleitung von 200 kW die Pressung 1500 N/mm² nicht übersteigt.
Für diese Berechnung wird eine Verzahnungsgeometrie gewählt, die für die Elektromobilität klassisch ist. Die maximale Breite des Radkörpers entspricht der Breite der Verzahnung (25 mm).
| Rad | Ritzel | |||
| Normaleingriffswinkel | αn | 20.00000 | 20.00000 | ° |
| Schrägungswinkel | β | -30.00000 | 30.00000 | ° |
| Zähnezahl | z | 43 | 21 | - |
| Achsabstand | a | 75.000 | 75.000 | mm |
| Normalmodul | mn | 2.00000 | 2.00000 | mm |
| Stirnmodul | mt | 2.30940 | 2.30940 | mm |
| Nennprofilverschiebungsfaktor | x | 0.571790 | - | |
| Zahnbreite | b | 25.000 | 32.000 | mm |
| Kopfkreisdurchmesser | da | 105.591 | 52.497 | mm |
| Profilüberdeckung | εα | 1.301 | 1.301 | - |
| Sprungüberdeckung | εβ | 1.989 | 1.989 | - |
| Gesamtüberdeckung | εγ | 3.291 | 3.291 | - |
Abbildung 1: Ergebnisse mit analytischem Vollscheibenradkörper (links) und Ergebnisse mit FE-Vollscheibenradkörper (rechts)
In Abbildung 1 sind die Ergebnisse der Berechnung dargestellt. In der linken Spalte werden die Ergebnisse mit analytischem Vollscheibenradkörper und in der rechten Spalte werden die Ergebnisse mit FE-Vollscheibenradkörper abgebildet. Dabei zeigt sich, dass die berechnete Lastverteilung über der Zahnbreite und auch die Ergebnisse für die 3D-Lastverteilung nahezu identisch sind.
Variation der Stegbreite des Radkörpers
Anhand des Beispiel-Reduktorgetriebes wird der Einfluss des Radkörpers auf die Verzahnung bestimmt. Hierzu werden im Folgenden verschiedene Radkörpergeometrien mit unterschiedlichen Stegbreiten erzeugt und die Ergebnisse verglichen. Zur weiteren Gewichtsreduktionen werden zusätzliche Bohrungen in den Radkörper eingebracht. Die Bohrungen sind so positioniert, dass diese direkt unter dem Zahneingriff in der Berechnung liegen. Der Einfluss des Radkörpers wird so maximiert und bildet ein Worst-Case-Szenario.
Der Radkörper ist als parametrisches CAD-Bauteil aufgebaut und wird für jede Berechnung erzeugt. Dabei wird der Radkranz mit 3* mn so dick angenommen, dass dessen Einfluss auf die Verzahnung als minimal angenommen werden kann (siehe ISO 6336-3 Bild 9). Die Nabe ist als Pressverband mit einer Nabenbreite ausgelegt, die der Zahnbreite entspricht. Der Außendurchmesser der Nabe ist so angepasst, dass auch bei kleinster Stegbreite das Drehmoment voll übertragen werden kann.
Variante 1: Stegbreite 25 mm
Variante 2: Stegbreite 15 mm
Variante 3: Stegbreite 10 mm
Variante 4: Stegbreite 5 mm
Abbildung 2: Radkörper mit unterschiedlichen Stegbreiten
Einfluss der Stegbreite auf die Breitenlastverteilung
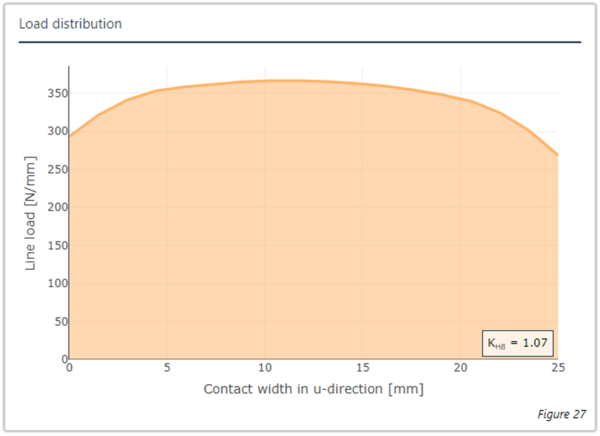
Durch die geringe Stegbreite können in Variante 4 (Stegbreite 5 mm) fast 50% des Gewichtes eingespart werden. Allerdings zeigt die Simulation deutlich, dass sich der Radkörper weicher verhält und damit weitere Verformungen in den Zahneingriff eingetragen werden, die bei der Korrektur mitberücksichtigt werden müssen.
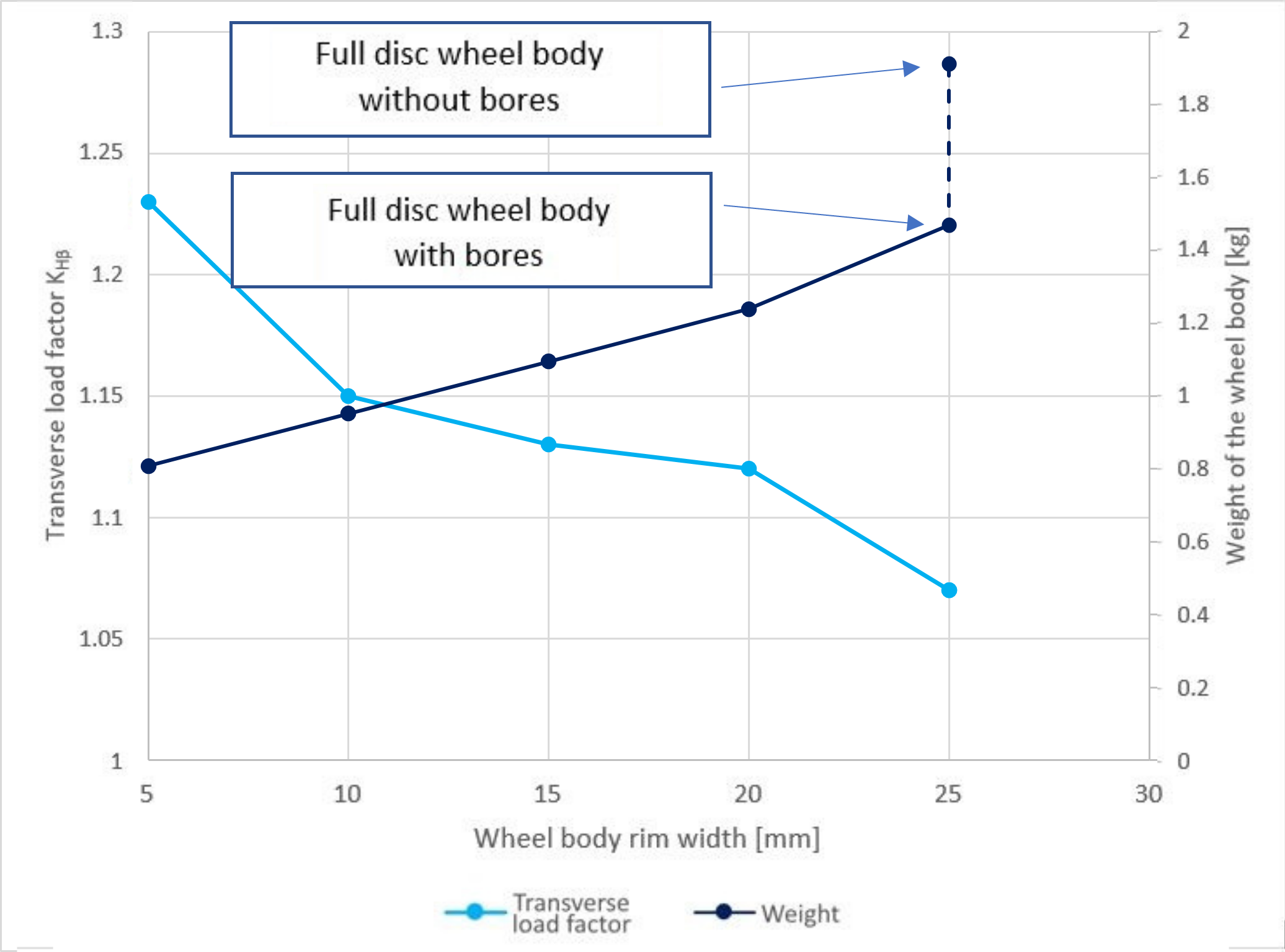
Abbildung 3: Gewicht und Breitenfaktor KHβ über der Stegbreite
In Abbildung 3 ist das Gewicht des Radkörpers und der daraus resultierende Breitenfaktor KHβ dargestellt. Die Auswertung zeigt, dass mit zunehmender Stegbreite der Breitenfaktor schnell abnimmt. In der Simulation konnte kein Unterschied zwischen einem Vollscheibenradkörper und einem ausgedrehten Radkörper mit einer Stegbreite von 20 mm festgestellt werden. Darüber hinaus sind allerdings starke Abweichungen zu beobachten, die bei der Korrektur berücksichtigt werden müssen. Die Änderungen im Zahnkontakt werden in Tabelle 1 aufgeführt. Es zeigt sich, dass moderate Stegbreiten den Breitenfaktor nur geringfügig beeinflussen.
| Stegbreite | Gewicht [kg] | Rel. Änderung | Breitenfaktor K_Hβ | Max. Pressung [N/mm²] |
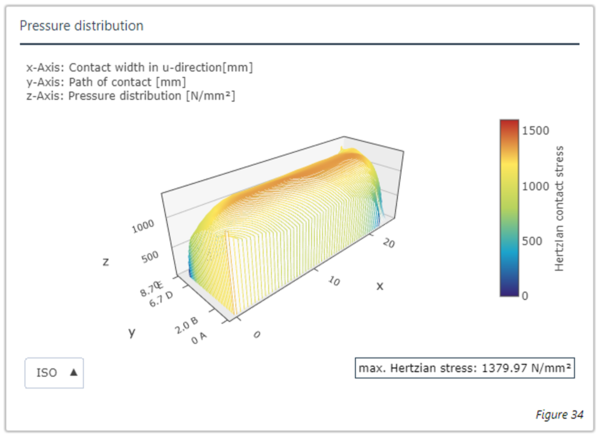
| 25 (mit Bohrung) | 1.91 | 0 % | 1.07 | 1473.92 |
| 25 (ohne Bohrung) | 1.47 | -23 % | 1.07 | 1611.59 |
| 20 | 1.24 | -35 % | 1.12 | 1706.46 |
| 15 | 1.1 | -42 % | 1.13 | 1899.43 |
| 10 | 0.9 | -50 % | 1.15 | 2188.90 |
| 5 | 0.8 | -58 % | 1.23 | 3171.81 |
Bei der maximalen Pressung jedoch wird bei 20 mm Stegbreite der Grenzwert von 1500 N/mm² örtlich begrenzt überschritten. Ab einer Stegbreite von 15 mm kommt es zu einer einseitigen Pressungsüberlastung und zu schadensrelevanten Pressungen auf der Flanke. Die zusätzlichen Deformationen, die aus der Radkörpersteifigkeit kommen, lassen sich durch eine einfache Schrägungswinkelkorrektur beheben. Der Korrekturvorschlag aus der FVA-Workbench weist den erforderlichen Korrekturbetrag für die Lastverteilung aus. Allerdings muss darauf geachtet werden, dass beim Wechsel von Zug- auf Schubbetrieb, das Drehmoment, bei gleicher Drehrichtung umkehrt. Für diesen Fall kommt die Rückflanke in Kontakt. Die Verzahnung kippt durch die Radkörpersteifigkeit in entgegengesetzte Richtung. Die Rückflanke muss entsprechend anders als die Vorderflanke korrigiert werden.
Fazit
Das Erhöhen der Leistungsdichte eines Getriebes kann relativ einfach über ein schmales Stegrad mit Bohrungen erreicht werden. Dadurch lassen sich am Rad deutliche Gewichtseinsparungen erzielen. Dies führt allerdings auch zu einer weicheren Konstruktion. Mit dem One-Click FEM-Verfahren der FVA-Workbench können auch Ungeübte schnell und zuverlässig FE-Berechnungen durchführen. Der geführte Berechnungsprozess hilft dabei, die gewünschten Effekte schnell und einfach zu berücksichtigen. Der Einfluss der Radkörpersteifigkeit ist bei komplexen Radkörpern deutlich sichtbar. Die Annahme eines Vollscheibenrades ist damit nicht mehr zulässig. Mit der FVA-Workbench lassen sich die zusätzlichen Verformungen einfach berechnen. Die vorgeschlagene Verzahnungskorrektur bezieht die zusätzliche Steifigkeit mit ein, sodass die Verzahnungskorrektur, die einen optimalen Betrieb sicherstellt, einfach ermittelt werden kann. Bei der Auslegung der Korrektur unter Berücksichtigung der Radkörpersteifigkeit müssen alle erwarteten Betriebspunkte mitberücksichtigt werden. Insbesondere der Wechsel von Zug- auf Schubbetrieb kann für die Verzahnung unzulässig hohe Pressungen im Kantenbereich zur Folge haben.