Radkörpergestaltung bei Kegelrädern
Bild: © FVA GmbHGrundlagen der Kegelradberechnung in der FVA-Workbench
Die FVA-Workbench bietet verschiedene Möglichkeiten zur Berechnung von Kegelrädern.
Einfache Verfahren werden mit gängigen ISO-, DIN- oder AGMA-Normen, Vorschriften der Schiffsklassifikationsgesellschaften und Berechnungen der FVA durchgeführt. Diese Ansätze rechnen mit Ersatzstirnradverzahnungen und sind daher auch ohne konkrete Fertigungsmaschine und detaillierte Geometrie sehr einfach anzuwenden. Allerdings bilden sie die Kegelradgeometrie nicht exakt ab. Genau an dieser Stelle setzt die lokale Simulation von Kegelrädern an. Im Gegensatz zu den einfachen Methoden basiert sie auf einer exakten Fertigungssimulation und auf einer Betrachtung aller Punkte im Eingriffsbereich. Durch den lokalen Ansatz können alle relevanten Einflüsse berücksichtigt werden, wie z. B. Wellenverlagerung, die Relativlage der Kegelräder zueinander und die umliegenden Steifigkeiten. Über einfache Sicherheitskennwerte hinaus können lokale Tragfähigkeitsnachweise einschließlich lokaler Schadensakkumulationsberechnungen oder Schadensfortschrittsberechnungen durchgeführt werden. Im vorliegenden Artikel geht es um Modellverbesserungen durch lokale Verzahnungsberechnungen.
Die Radkörpergestaltung in der FVA-Workbench
Die Berechnung der Lastverteilung an Kegel- und Hypoidrädern wird maßgeblich durch die umliegende Steifigkeit beeinflusst. Berücksichtigt wird die Steifigkeit der umliegenden Lager, der Welle, des Zahns und des Radkörpers.
Bisher wurde die Steifigkeit des Radkörpers in der FVA-Workbench durch einen elastischen Halbraum angenähert. Im Forschungsprojekt FVA 223 XVI „Methode zur Einbeziehung der Steifigkeit komplexer Radkörper in die Lastverteilungsberechnung und deren Umsetzung in BECAL“ (IMM der TU Dresden, Prof. Dr. Schlecht, CAD der Universität Bayreuth, Prof. Dr. Rieg) wurden Methoden entwickelt, die Steifigkeit des Radkörpers präzise durch ein passendes FE-Modell zu ergänzen. Mit diesem Modell können Bohrungen im Radkörper, die Position, an der das Rad an der Welle befestigt ist, und die Geometrie des Radkörpers exakt mitberücksichtigt werden.
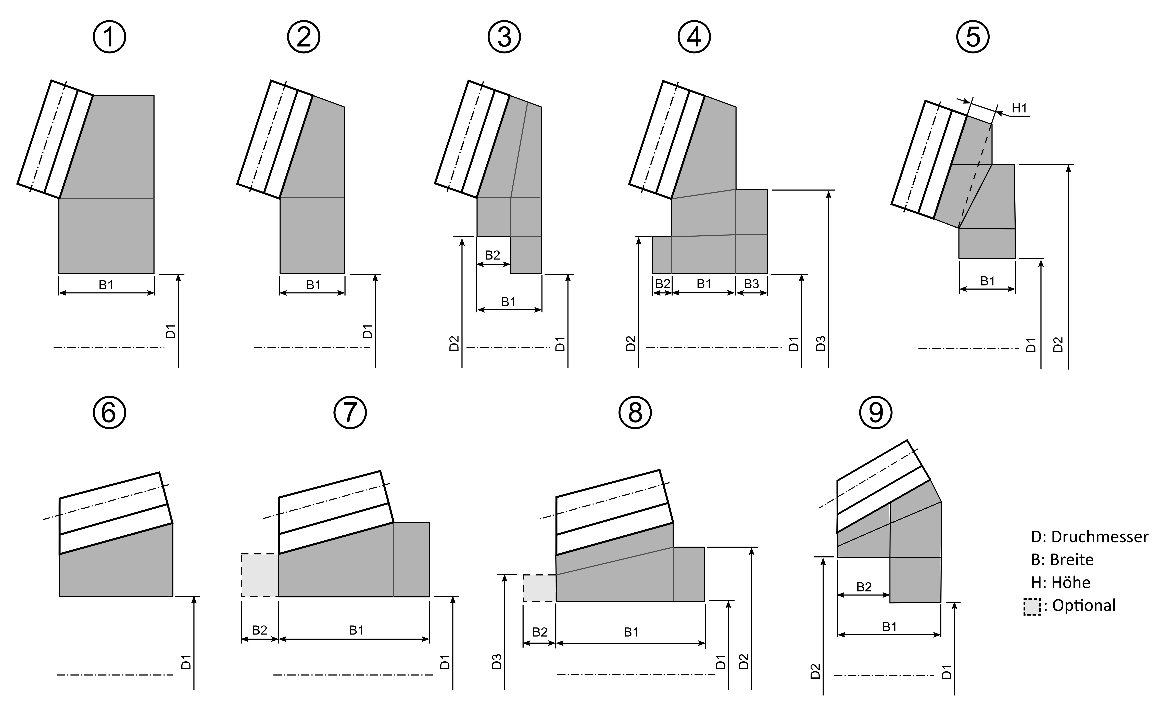
Berücksichtigung der Radkörperverformungen in der frühen Auslegungsphase mit parametrisierbaren Standard-Radkörpern: In der frühen Auslegungsphase ist die genaue Radkörpergeometrie oftmals noch nicht finalisiert. Daher lassen sich im ersten Schritt Radkörper parametrisch erstellen. Aus einer Auswahl von 9 Standard-Radkörpern und 6 verschiedenen Einspannmöglichkeiten lassen sich alle wichtigen Größen parametrisch definieren. Damit können in der FVA-Workbench sehr schnell und einfach erste Abschätzungen zum Einfluss des Radkörpers in sehr frühen Phasen des Projekts durchgeführt und damit zeit- und kostenintensive Änderungen an der Konstruktion vermieden werden. Die Eingabe in der FVA-Workbench wird durch zahlreiche Skizzen und Hilfetexte unterstützt. Um den Projektfortschritt zu unterstützen lassen sich die Radkörper als CAD-Bauteile exportieren. Damit kann der Konstrukteurin oder dem Konstrukteur eine Grundkonstruktion zur Verfügung gestellt werden, die nur noch ausdetailliert werden muss.
Abbildung 1: Darstellung der parametrischen Radkörpermöglichkeiten in der FVA-Workbench
Abbildung 2: Darstellung der parametrischen Einspannmöglichkeiten in der FVA-Workbench
Konfiguration der Einspannungsbereiche
Standardmäßig ist beim Ritzel die Ferseneinspannung (1) und beim Tellerrad die Nabeneinspannung (0) gewählt. Eine weitere Einspannungsmöglichkeit ist die Zeheneinspannung 2. Mit den Optionen 3 - 6 ist eine Kombination der Einspannungsbereiche möglich.
Parametrisierbare Standard-Radkörper
Für eine gute Vernetzungsqualität wird empfohlen, die Varianten 1-5 als typische Tellerradradkörper und die Varianten 6-9 als typische Ritzelradkörper einzusetzen. Standardmäßig wird für das Ritzel die Variante 6 und für das Tellerrad die Variante 1 gewählt.
Abbildung 3: Tellerrad mit komplexen CAD-Radkörper und Ritzel mit Standardradkörper in der FVA-Workbench
Berücksichtigung der Verformungen komplexer Radkörpergeometrien im fortgeschrittenen Entwicklungsprozess
Alle Radkörper können als CAD-Modell eingelesen und verarbeitet werden. Der erste Schritt dabei ist die Positionierung. Die Positionierung stellt sicher, dass das Bauteil später an der richtigen Stelle sitzt und macht die CAD-Konstruktion unabhängig von der späteren Berechnung. Bei der Positionierung wird das CAD-Modell zugeschnitten, wodurch sichergestellt werden kann, dass die Schnittfläche genau auf die Verzahnung passt und ggf. enthaltene Zähne auf dem Radkörper weggeschnitten werden. Mathematisch entspricht der Positionierungsvorgang einer Koordinatentransformation. Die grafische Unterstützung stellt sicher, dass bei diesem komplexen Prozess keine Fehler passieren.
Im nächsten Schritt wird das Bauteil vernetzt. Die Netzqualität wird von der FVA-Workbench überwacht und sobald zu viele verzerrte oder ungeeignete Elemente entstehen, wird eine Warnung ausgegeben. Über den FEM Qualitäts-Checker kann einfach festgestellt werden, an welchen Stellen ungünstige Elemente entstehen. Diese können dann im CAD Modell entfernt oder durch eine feinere Vernetzung aufgelöst werden. Abschließend werden die Koppelknoten definiert. Das Fangen der Koppelknoten ist ein automatischer Prozess, der alle FEM-Knoten markiert, die die Verzahnung oder die Welle berühren.
Die örtliche Tragfähigkeitsberechnung unter Berücksichtigung von Radkörperverformungen
Die örtliche Tragfähigkeitsberechnung besteht aus einer Vielzahl an Berechnungsschritten, die automatisch abgearbeitet werden. Die Grundlage bildet die exakte Geometrie der Kegelradzähne, einschließlich aller topologischen Modifikationen. Diese exakte Geometrie wird entweder aus der Fertigungssimulation auf Grundlage der Maschineneinstelldaten berechnet oder durch Import der Oberflächenbeschreibung in Form einer Punktewolke (3D-Neutraldaten) eingelesen. Die Relativlageabweichungen unter Last, die durch Gehäuseverformungen, Wellendurchbiegung und Lagereinsenkung während der Betriebszeit auftreten, kommen aus der Gesamtsystemberechnung. Mit der exakten Verzahnungsgeometrie und unter den ermittelten Relativlageabweichungen wird der Zahnkontakt simuliert. Die so berechneten Kontaktverhältnisse können als Ease-Off, Tragbild und Drehfehler visualisiert werden. Sogenannte Klaffmaße beschreiben die Kontaktabstände zwischen den Zähnen entlang der Traglinien unter Beachten von Wälzabweichung, Mehrfacheingriff und Voreingriff. Darauf baut die Lastverteilungsberechnung auf. Die Steifigkeitsverhältnisse von Kegelradverzahnungen mit elastischem Radkörper werden hier durch die Summe aus BEM- und FEM-Einflusszahlen abgebildet. Die Radkörperelastizität steckt in den FEM-Einflusszahlen. Ebenso neu ist, dass bei modellierten Radkörpern die Koppeleinflüsse aller im Eingriff befindlichen Zähne berücksichtigt und der Einflusszahlenmatrix hinzugefügt werden. Aus der örtlichen Lastverteilungsberechnung und den Kontaktverhältnissen folgen schließlich die örtlichen Beanspruchungen sowie die Fußspannungen über der Zahnbreite und daraus werden entsprechende örtliche Tragfähigkeitswerte und Sicherheiten ermittelt.
Einflüsse aus der Radkörpergestaltung auf die Flankenlastverteilung
Einfluss der Tellerrad-Radkörperbreite
Die Breite des Radkörpers hat einen direkten Einfluss auf die Steifigkeit der Verzahnung und damit auf das Ergebnis. Im Folgenden soll der Einfluss der Breite des Radkörpers am Rad auf die Pressungsverteilung und die Zahnfußspannung diskutiert werden. Dazu wird mit Hilfe der Standardradkörper ein parametrisches Modell in der FVA-Workbench aufgebaut, welches sich sehr leicht anpassen und erneut rechnen lässt. In diesem Modell wird der Radkörper des Rades in der Breite variiert und die Ergebnisse gegeneinander verglichen. Nach unten hin wird die Radkörperbreite dahingehend begrenzt, dass die FE-Vernetzung eine minimale Kranzdicke von einem Profilschnittmodul benötigt. Ein dünnerer Radkörper ist nur mit einer individuellen Konstruktion möglich.
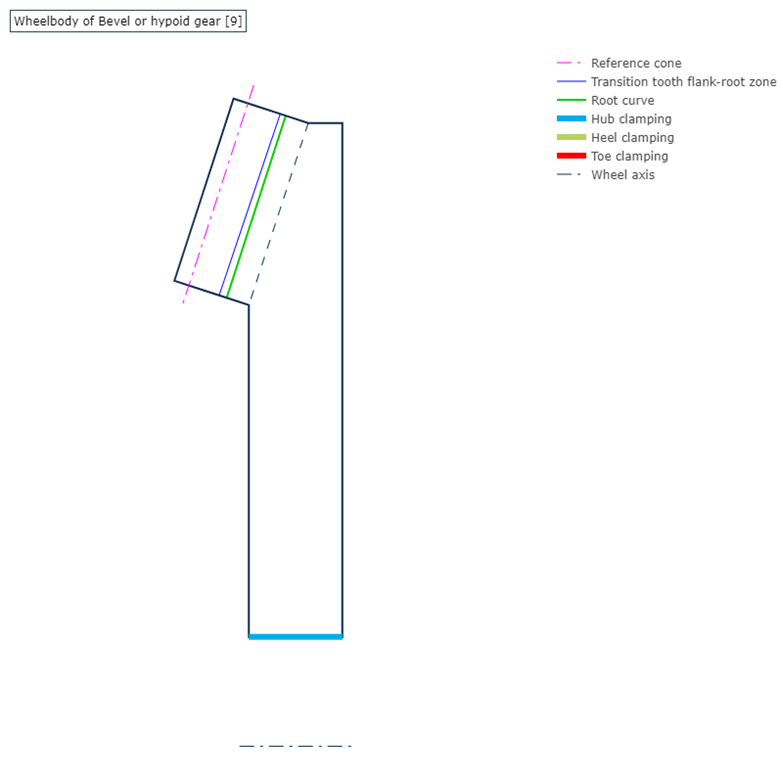
Die Radkörpergeometrie für die dickste und die dünnste Variante wird in den Abbildungen 4 und 5 dargestellt. Die türkisfarbene Linie stellt die Fesselungsrandbedingung an der Nabe dar. Hier wird der Radkörper an der Welle festgehalten.
Abbildung 4: Radkörpergeometrie – Darstellung im Report der FVA-Workbench; Radkörperbreite 17,1 mm
Abbildung 5: Radkörpergeometrie – Darstellung im Report der FVA-Workbench; Radkörperbreite 50 mm
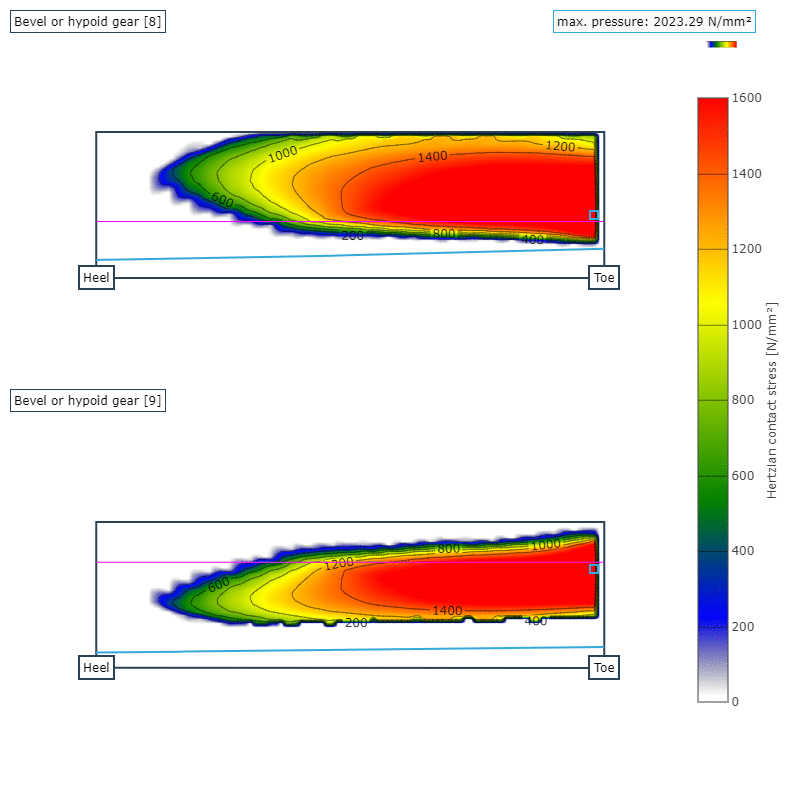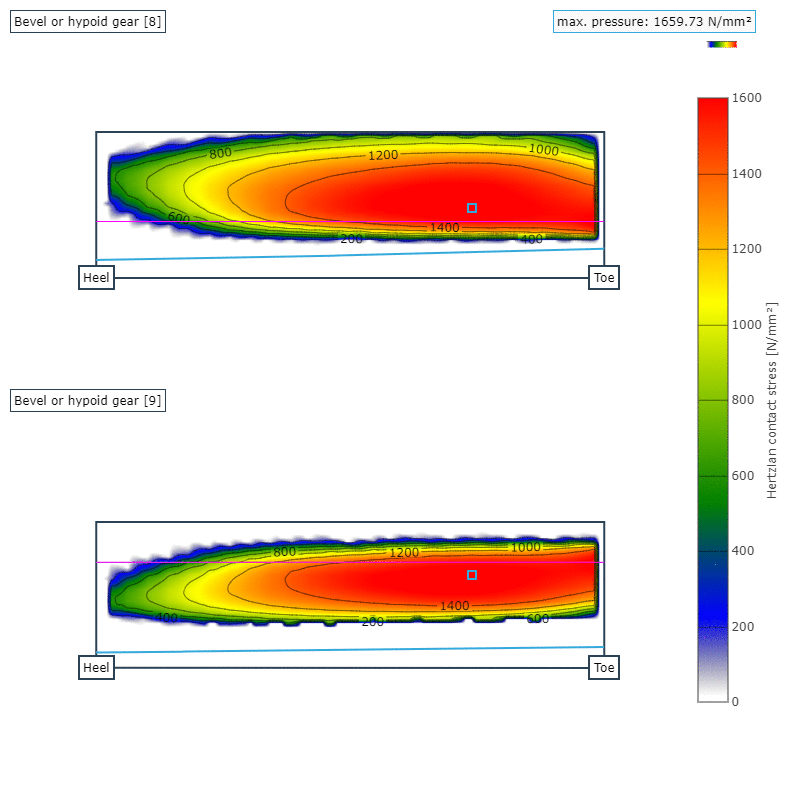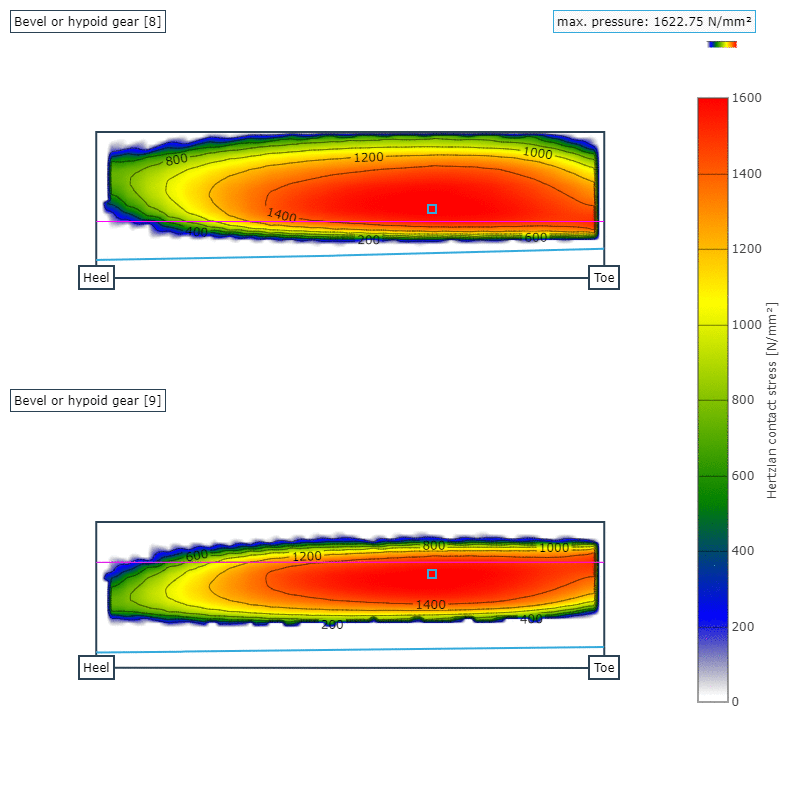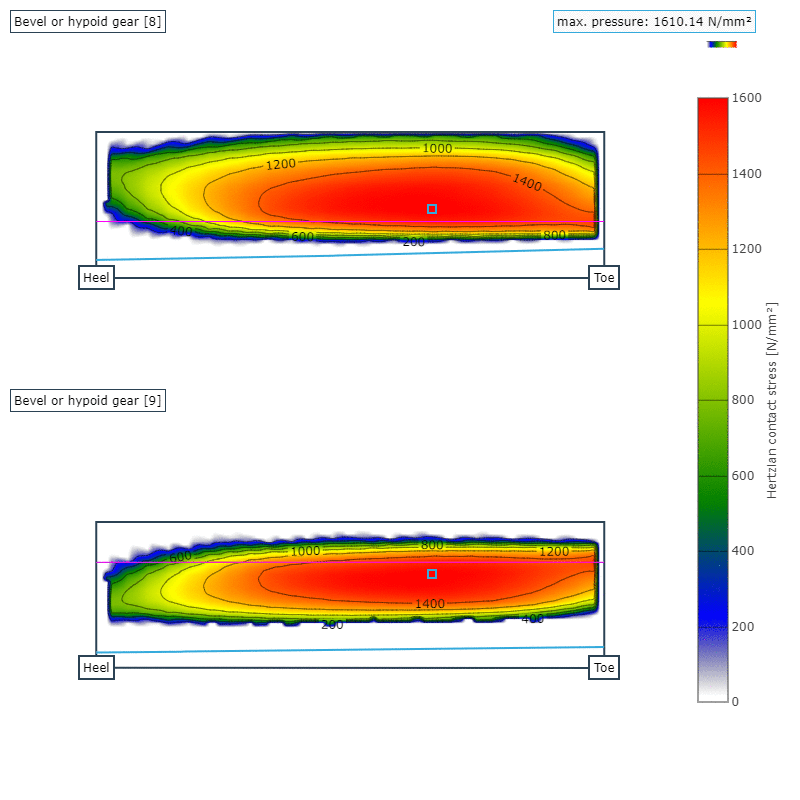
Abbildung 6: Auswirkung der Radkörperbreite des Tellerrades auf die maximalen Hertzschen Pressung auf der Ritzel- (oben) und der Tellerradflanke (unten); Radkörperbreite 17,1 mm
Abbildung 7: Auswirkung der Radkörperbreite des Tellerrades auf die maximalen Hertzschen Pressung auf der Ritzel- (oben) und der Tellerradflanke (unten); Radkörperbreite 50 mm
In den Abbildungen 6 und 7 ist die Pressungsverteilung auf der Zahnflanke für einen Radkörper mit der Breite 17,1 mm und für 50 mm dargestellt. Im direkten Vergleich wird deutlich, dass durch die geringe Steifigkeit des Radkörpers die Zähne nicht mehr optimal in den Eingriff kommen und ein Kantenträger mit deutlichen Spannungsüberhöhungen entsteht. Dies legt den starken Einfluss des Radkörpers auf das gesamte Betriebsverhalten nahe.
Abbildung 8: Verlauf der Zahnfußsicherheit über der Radkörperbreite
In Abbildung 8 ist die Zahnfußsicherheit über der Radkörperbreite aufgetragen. Mit zunehmender Breite des Radkörpers wird deutlich, dass die Zahnfußsicherheit weiter degressiv wächst. Im Rahmen einer solchen Betrachtung lässt sich ein Optimum aus der Masse und einer ausreichenden Sicherheit bilden.
Den Einfluss des Radkörpers einfach mit der FVA-Workbench berücksichtigen
Mit der FVA-Workbench lässt sich der Einfluss der Radkörpersteifigkeit für den Kegelradeingriff vollständig beschreiben. Eine Überdimensionierung mit bekanntem „Angst-Eisen“ ist nicht mehr notwendig. Mit dem Kegelradmodul kann einfach und präzise simuliert werden, wo kritische Betriebsbedingungen auftreten und wie diese konstruktiv gelöst werden können.
Vergleicht man die Pressungsverteilungen bei den beiden Radkörperbreiten, wird deutlich, dass die dünnere Konstruktion zu einem starken Kantenträger führen wird. Eine Berücksichtigung der Radkörpersteifigkeit ist damit unerlässlich bei der Auslegung der Verzahnung.
Die Möglichkeit parametrische Radkörper in der FVA-Workbench zu definieren, macht es sehr einfach, den Radkörpereinfluss schon in frühen Produktentwicklungsphasen mit zu berücksichtigen. Auf diesem Weg lassen sich sowohl Änderungskosten als auch eine Überdimensionierung vermeiden.