Bestimmung der Breitenlastverteilung von Planetenstufen
Bild: © Center for Wind Power Drives, RWTH AachenDas Ziel, die Leistungsdichte eines Getriebes zu erhöhen, setzt voraus, dass überschüssige Materialreserven erkannt und auf das notwendige Maß reduziert werden können. In diesem Zusammenhang ist es wichtig zu wissen, welche Einflüsse auf das Getriebe wirken und welche Belastungen daraus resultieren. Dabei spielt die genaue Kenntnis der sich im Betrieb ergebenden Breitenlastverteilung in den Zahneingriffen und deren Optimierung über die Vorgabe geeigneter Mikrogeometrien eine entscheidende Rolle.
Am Beispiel eines Planeten-Stirnradgetriebes aus dem Forschungsprojekt FVA-Gondel [1], wie es typischerweise für Windenergieanlagen von Leistungen bis zu bis 1,5 MW zum Einsatz kommt, wird die realitätsnahe Bestimmung der Breitenlastverteilung in Planetenstufen und die Ermittlung der sich daraus ergebenden, notwendigen Breitenkorrekturen mit Hilfe der FVA-Workbench dargestellt. Dabei soll im Wesentlichen der Einfluss der Planetenträgersteifigkeit quantifiziert und berücksichtigt werden.
Berechnung der Breitenlastverteilung von Planetenstufen
Die Breitenlastverteilung in einer Planetenstufe wird hauptsächlich durch die folgenden Einflüsse bestimmt:
Torsionsverformung des Sonnenritzels
Durchbiegung des Planetenbolzens
Verdrillung der Planetenwangen (bei zweiwangigen Planetenträgern)
Durchsenkung und Spiele der Planetenlager (insbesondere bei Schrägverzahnungen)
Die Torsionsverformung lässt sich sehr gut mit den in den Normen angegebenen Formeln berechnen. Dies gilt näherungsweise auch noch für die Biegeverformung des Planetenbolzens. In vereinfachten Berechnungsverfahren, die im Wesentlichen auf den in den Tragfähigkeitsnormen beschriebenen Methoden basieren, stellen diese beiden Verformungsbeträge die Haupteinflüsse auf die Breitenlastverteilung dar.
Das Verformungsverhalten von Planetenträgern kann dagegen nicht mehr mit ausreichender Genauigkeit durch vereinfachte Formeln beschrieben werden, sodass hier auf die Finite Elemente Methode zurückgegriffen werden muss, um realistische Ergebnisse zu erzielen.
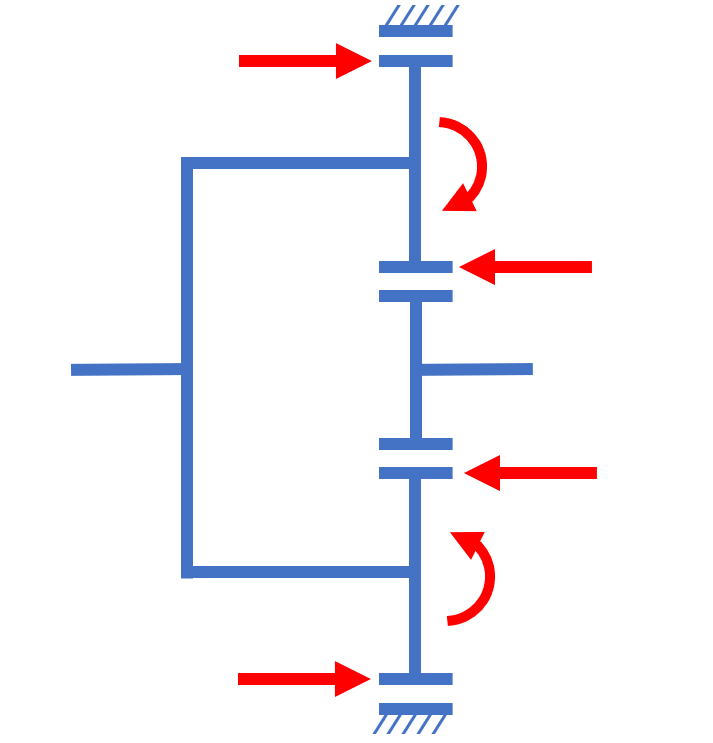
Zusätzlich führen bei schrägverzahnten Planetenrädern die sich gegenüberstehenden Axialkräfte in den Zahneingriffen Sonne-Planet und Planet-Hohlrad zu einer Verkippung der Planeten innerhalb der elastischen Lagerdurchsenkungen und der Radialspiele der Planetenlager. Auch für diese Beträge sind in den Normen keine Näherungsformeln vorhanden, sodass sie detailliert auf Basis der Lagergeometrie und der Lastverteilung im Lager ermittelt werden können.
Abbildung 1: Planetenradverkippung
Berücksichtigung der Planetenträgerverformung in der FVA-Workbench
Zur Berücksichtigung der Planetenträgerverformung stellt die FVA-Workbench vier verschiedene Möglichkeiten zur Verfügung.
1. Option: Die Wangen des Planetenträgers werden vereinfacht durch verwindungssteife Vollscheiben abgebildet. Bei zweiwangigen Planetenträgern erfolgt die Drehmomentübertragung zwischen den beiden Wangen über die Bolzen und die Eingabe einer zusätzlichen Verdrehsteifigkeit zwischen den Wangen, falls diese aus externen Berechnungen oder aus Messungen vorliegt.
2. Option: Der Planetenträger wird in der FVA-Workbench modelliert, indem die Wangen und Bolzen als Vollscheiben bzw. Vollwellen angenähert werden. Bei zweiwangigen Planetenträgern können zusätzliche verschiede Formen von Streben zwischen den beiden Wangen definiert werden. Danach erfolgt innerhalb der FVA-Workbench eine automatisierte Vernetzung dieser Geometrie mit einer anschließenden Berechnung der Planetenträgerverformung mit dem Finit-Elemente-Solver [2].
3. Option: Liegt bereits ein auskonstruierter Planetenträger in Form einer CAD-Datei vor, so kann dieser in die FVA-Workbench eingeladen werden. Auch hier erfolgt dann eine automatisierte Vernetzung mit anschließender Verformungsberechnung mittels der FE-Methode. In Abbildung 2a ist beispielhaft ein verformter Planetenträger und in Abbildung 2b die sich daraus ergebende Durchsenkung des Planetenbolzen dargestellt.
4. Option: Falls bereits eine externe Verformungsberechnung des Planetenträgers durchgeführt wurde, kann das so ermittelte Verformungsverhalten in der FVA-Workbench über das Einlesen einer reduzierten Steifigkeitsmatrix im Harwell-Boeing-Format berücksichtigt werden.
Abbildung 2a: Verformter Planetenträger
Abbildung 2b: Planetenbolzendurchsenkung
Die Verlässlichkeit der Ergebnisse bei der Berechnung von Bauteilen mittels der FE-Methode hängt sehr stark von der geeigneten Wahl der Randbedingungen und der Vernetzung ab. In der FVA-Workbench läuft die Vernetzung des Bauteils und Festlegung der Koppelpunkte weitgehend automatisiert ab (One-Click-FEM-Verfahren) und ist speziell auf die zu berechnenden Getriebebauteile angepasst. Das Einladen und die Positionierung der Bauteile erfolgt in der FVA-Workbench im 3D-Modell und wird durch eine geeignete Benutzerführung unterstützt. Diese Vorgehensweise stellt sicher, dass auch ohne spezielle FE-Kenntnisse zuverlässige und reproduzierbare Ergebnisse erzielt werden können.
Berechnung der Steifigkeiten und Betriebsspiele von Wälzlagern in der FVA-Workbench
In der FVA-Workbench wird die Steifigkeit und das Betriebsspiel der Wälzlager mit in FVA-Forschungsvorhaben entwickelten Methoden [3,4] berechnet. Diese basieren auf einer detaillierten Kontaktanalyse zwischen den Wälzkörpern und den Lagerringen. Im Rahmen der Forschungsvorhaben wurden diese Methoden durch Prüfstandsversuche und Abgleich mit den Berechnungen der Lagerhersteller validiert.
Abbildung 3: Lastverteilung in einem Planetenlager
Berechnungsbeispiel
Die Wichtigkeit einer detaillierten Verformungsanalyse zur Berechnung der Breitenlastverteilung und Auslegung von Breitenkorrekturen in Planetenstufen wird im Folgenden am Beispiel des in der FVA-Gondel [1] verwendeten Getriebemodells veranschaulicht. In Abbildung 4 wird dazu die Breitenlastverteilung der Planetenstufe im Eingriff Sonne-Planet für drei unterschiedliche Berechnungsvarianten gegenübergestellt:
Variante 1: Hier ist die Breitenlastverteilung auf Basis einer vereinfachten Berechnung ohne Berücksichtigung der Planetenträgerverformung und der Durchsenkung der Planetenlager dargestellt, so wie sie vielfach noch in vereinfachten Methoden verwendet wird. In der FVA-Workbench kann dazu die Verdrehsteifigkeit des Planetenträgers und die Radialsteifigkeit der Planetenlager auf einen sehr großen Wert gesetzt werden. Es ist zu erkennen, dass hier die Torsionsverformung des Sonnenritzels (blaue Fläche) gegenüber der Verkippung des Planeten (grüne Fläche) dominiert. Diese Vorgehensweise liefert eine rechnerische Lastüberhöhung am generatorseitigen Zahnende.
Variante 2: In dieser Berechnung ist zusätzlich eine Breitenkorrektur in Form eine Schrägungswinkelmodifikation mit einer symmetrischen Breitenballigkeit berücksichtigt. Die Breitenkorrektur ist so gestaltet, dass diese zusammen mit den Verformungen aus der vereinfachten Berechnung in Variante 1 eine ausgeglichene Breitenlastverteilung ergibt.
Variante 3: Diese Breitenlastverteilung ergibt sich aus der detaillierten Berechnung der Verformungen des Planetenträgers und der Planetenlager, wenn diese durch die aus der vereinfachten Berechnung ermittelten Flankenkorrekturen kompensiert werden sollen. Es ist zu erkennen, dass in diesem Fall die größere Verkippung des Planetenrades zu einer lokalen Überlastung am rotorseitigen Verzahnungsende führt.
Abbildung 4: Lastverteilung im Eingriff Sonne-Planet (links) und Verformungsbeträge entlang der Zahnbreite (rechts)
In Planetenstufen, in denen eine mittels vereinfachter Methoden ausgelegte Verzahnungskorrektur mit niedrigen Materialreserven kombiniert ist, können sich Schadensbilder mit großflächiger Pittingbildung am rotorseitigen Verzahnungsende des Sonnenritzels ergeben. Abbildungen 5a und 5b zeigen beispielhaft ein derartiges, auf eine lokale Lastüberhöhung zurückzuführendes Schadensbild einer Sonnenritzelwelle aus einem Hauptgetriebe einer Windenergieanlage der Leistungsklasse 1,5 MW, das einen zu dem verwendeten Berechnungsmodell vergleichbaren konstruktiven Aufbau aufweist.
Abbildung 5a: Praxisbeispiel eines beschädigten Sonnritzels
Abbildung 5b: 3D-Pressungsverteilung der Variante 3
Fazit
Mit der FVA-Workbench lassen sich auf einfache Weise alle relevanten Einflüsse bei der Auslegung von Verzahnungskorrekturen in Planetenstufen berücksichtigen. Damit ist es eine gewichts- und kosteneffiziente Konstruktion möglich und es kann gleichzeitig eine hohe Betriebssicherheit gewährleistet werden.
Referenzen
[1] FVA-Vorhaben 730 - Belastungen an den Antriebskomponenten von Windenergieanlagen
[2] FVA-Vorhaben 711 I: Einbindung elastischer Gehäusestrukturen in die Getriebeauslegung mit RIKOR und Visualisierung des Getriebegesamtsystems in der FVA-Workbench
[3] FVA 364 bis V – Unterprogramm LAGER 2
[4] FVA-Vorhaben 909 – Transfer Wälzlagerberechnung