Einfluss der Ziehbarkeit von Kegelritzeln auf die Gehäusegestaltung
Die FVA-Workbench ist ein herstellerneutrales Werkzeug zur Simulation und Berechnung von Getriebesystemen. Bei kürzer werdenden Produktentwicklungszyklen ist es besonders wichtig, auf performante Modellierungsansätze und Berechnungsalgorithmen zu setzen. Die vorwiegend analytischen Ansätze garantieren schnelle und verlässliche Lösungen für alle wichtigen Fragen der Antriebstechnik. Ergebnisse von analytisch nicht beschreibbaren Körpern werden um geeignete nummerische Verfahren ergänzt. Die intuitive Modellierungstechnik der FVA-Workbench garantiert stets ein vollständiges, valides und herstellbares Getriebe.
Entwickelt, diskutiert und validiert werden die Berechnungen in Forschungsvorhaben der Forschungsvereinigung Antriebstechnik e.V. (FVA). Durch Mitgliedsbeiträge und öffentliche Förderungen werden in der FVA jährlich 14 Mio. Euro in Forschungsvorhaben an den besten deutschen Universitäten, Lehrstühlen und Forschungseinrichtungen umgesetzt. Die FVA-Workbench versteht sich hier als Wissensplattform, um das Wissen der FVA für jeden Ingenieur zugänglich zu machen.
Jetzt die FVA-Workbench kostenfrei ausprobieren
Testen Sie den vollen Funktionsumfang der FVA-Workbench für 6 Wochen und überzeugen Sie sich selbst.
Grundlagen der komplexen Kegelradberechnung in der FVA-Workbench – Lastfreie Zahnkontaktsimulation
Neben Beanspruchung, Tragfähigkeit und den Schadenssummen können mit präzisen Tragfähigkeitsberechnungen von Kegelradstufen noch weitere Eigenschaften ermittelt werden. Insbesondere das Potential der lastfreien Zahnkontaktsimulation und deren Einfluss auf den Auslegungsprozess spielt eine entscheidende Rolle.
Ausgangspunkt jeder Berechnung ist die exakte Oberfläche für Kegel- und Hypoidräder und ihre Relativlage zueinander. Die Beschreibung von Zahnflanke und Zahnfuß wird aus einer Herstellsimulation generiert und berücksichtigt die Maschineneinstelldaten und Fertigungsabweichungen. Über Ausgleichsflächen wird aus dieser diskreten Punktewolke eine lückenlose mathematische Zahnoberflächenbeschreibung.
Die Abwälzsimulation, als Kernstück der lastfreien Zahnkontaktsimulation, kann somit sehr effizient die wichtigsten Größen der Verzahnung bestimmen. Maßgebliche Beurteilungsgrößen sind: der Ease-Off, die lastfreie Wälzabweichung, das Leerlauftragbild, die Bestimmung des Flankenspiels und der axialen Ziehbarkeit des Ritzels (Forschungsvorhaben FVA 456 II „BECAL- Flankenspiel und Ziehbarkeit“, IMM der TU Dresden, Prof. Dr. Schlecht).
Das Verdrehflankenspiel wird in Abhängigkeit der Verzahnungsgröße, der Fertigungsqualität sowie der unter Last zu erwartenden Relativlageänderungen gewählt. Damit werden Eingriffsstörungen und Klemmen der Verzahnung verhindert. Ein zu geringes Verdrehflankenspiel kann durch die unter Last zu erwartenden Relativlageänderungen zum Klemmen führen, ein zu großes Flankenspiel zu erhöhten Laufgeräuschen und verminderter Tragfähigkeit.
Bei der Berechnung des Verdrehflankenspiels werden zusätzlich zur Mikrogeometrie die Einbaulage sowie die Relativlageänderungen unter Last und die angegebenen Teilungsabweichungen der Arbeits- und Rückflanken berücksichtigt.
Da Kegelräder in der Praxis immer Flankenmodifikationen besitzen, ist das Verdrehflankenspiel über den Eingriffsstellungen betrachtet, nicht konstant (siehe Abbildung 1). Die Differenz zwischen minimalem und maximalem Verdrehflankenspiel entsteht durch eine Überlagerung der Wälzabweichungen von Schub- und Zugbetrieb. Die theoretischen Grundlagen zur Verdrehflankenspielberechnung wurden im FVA-Projekt FVA 223/XVIII („BECAL - Betriebsflankenspiel“, IMM der TU Dresden, Prof. Dr. Schlecht) entwickelt und implementiert. In aktuell laufenden Forschungsvorhaben werden die Einflüsse rund um die Flankenspielberechnung neu bewertet, um die realen Bedingungen unter Last noch besser abzubilden.
| Grundgeometriegröße | Ritzel | Tellerrad |
| Zähnezahl | 15 | 43 |
| Normalmodul | 3.18 mm | |
| Achswinkel | 90° | |
| Achsversatz | 0.0 mm | |
| Zahnbreite | 35 mm | 35 mm |
| Mittlere Teilkegellänge | 88.41 mm | 88.41 mm |
| Mittlerer Schrägungswinkel | 35° -35° |
Eine weitere Anwendung der Verdrehflankenspielberechnung ist die Bewertung der Ziehbarkeit des Ritzels. Ein Ritzel ist ziehbar, wenn man es aus dem Eingriff herausdrehen kann und das Ritzel nur entlang der Radachse bewegt. Die Relativlage der Radachse des Ritzels verändert sich folglich nur in axialer Richtung aus dem Eingriff heraus. Ziehbarkeit beschreibt sowohl den Montage- als auch den Demontagevorgang. Dies hat einen enormen Einfluss insbesondere auf die Gehäusegestaltung. Die Frage, ob axiale Ziehbarkeit des Kegelritzels vorliegt oder nicht, beeinflusst die Montage- und Demontagevorgänge erheblich.Die Ziehbarkeit berechnet sich aus dem Verdrehflankenspiel. Daher gehen auch hier die exakte Zahnform inklusive Mikrogeometrie und Abweichungen aus der Fertigung ein. Den größten Einfluss auf die Ziehbarkeit hat der Messerkopfradius rc0, da dieser die Krümmung der Flanke in Längsrichtung bestimmt. Dieser sollte zu aller erst angepasst werden, wenn die Ziehbarkeit optimiert werden soll. Große Messerkopfradien erhöhen die Ziehbarkeit, können aber nicht beliebig vergrößert werden, da diese durch wirtschaftliche Gesichtspunkte und eine Veränderung des Verlagerungsverhaltens begrenzt werden.
In der FVA-Workbench wird als Ergebnis der Ziehbarkeitsberechnung das minimale und maximale Verdrehflankenspiel über der axialen Ritzelverschiebung grafisch dargestellt. Dabei können folgende drei Fälle auftreten:
Ziehbarkeit: Die Kurven des minimalen und maximalen Verdrehflankenspiel sind monoton steigend. Die Minima liegen im Koordinatenursprung.
Bedingte Ziehbarkeit: Das Minimum des minimalen Verdrehflankenspiel ist negativ und das Minimum des maximalen Verdrehflankenspiel ist positiv. Das bedeutet, in den entsprechenden axialen Ritzelpositionen gibt es Eingriffsstellungen, in denen sich Ritzel und Tellerrad nicht durchdringen. Nur unter idealen Bedingungen kann durch Verdrehen von Ritzel und Tellerrad zueinander, während der axialen Ritzelverschiebung, ein Klemmen verhindert werden. Ohne nähere Prüfung ist keine Ziehbarkeit anzunehmen.
Keine Ziehbarkeit: Die Minima sind negativ. Das heißt, für alle axialen Ritzelpositionen mit negativem minimalen und maximalen Verdrehflankenspiel wird in allen Eingriffsstellungen eine Durchdringung berechnet. Die Verzahnung klemmt und das Ritzel kann nicht axial bewegt werden.
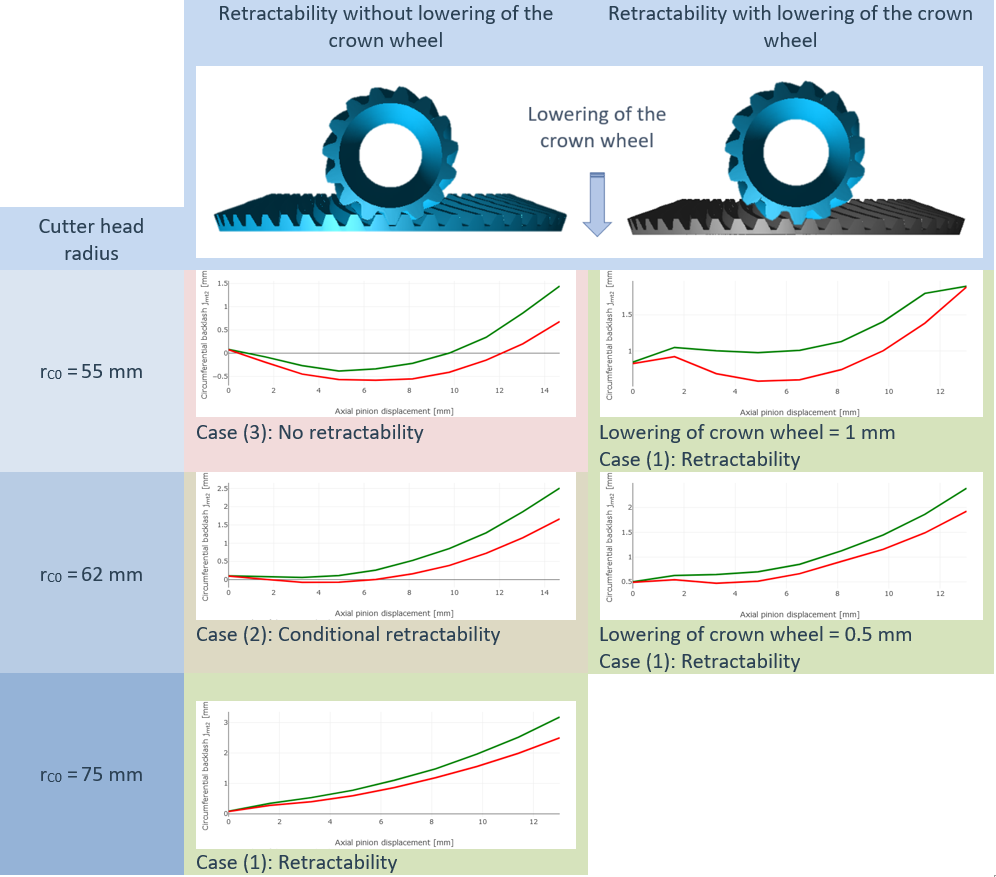
Für eine Kegelradverzahnung mit der Grundgeometrie gemäß Tabelle 1 sind Ergebnisse zur Ziehbarkeit in der Abbildung 3 zusammengefasst dargestellt.
Wenn keine Ziehbarkeit vorliegt, so kann eine Montage erfolgen, in dem das Ritzel in Achsrichtung der Tellerradachse in den Eingriff gelegt wird. Oder hier wird konstruktionsseitig das Absenken des Tellerrades (axiale Verschiebung des Tellerrades aus dem Eingriff heraus) vorgesehen. Unter dieser Bedingung kann die axiale Ziehbarkeit des Ritzels erreicht werden (siehe Abbildung 3). Dazu ist bei der Ziehbarkeitsberechnung die Eingabe der Tellerradabsenkung vorgesehen, um zu prüfen, ob der vorgesehene Wert ausreichend ist.
Die Berechnung der Ziehbarkeit bereits in der Auslegungsphase, lässt somit wichtige Rückschlüsse für die Gestaltung und die Anforderungen an das Getriebeumfeld (Gehäuse) zu. Liegt bei der Kegelradauslegung keine Ziehbarkeit vor, kann sie durch Konstruktions- oder Auslegungsänderungen hergestellt werden. Die Wirksamkeit dieser Änderungen lässt sich schnell und effizient mit der FVA-Workbench nachrechnen.
Abbildung 1: Mittleres Verdrehflankenspiel im Stirnschnitt dargestellt über dem Tellerraddrehwinkel für zwei Teilungen (Grafik-Ausgabe der FVA-Workbench)
Abbildung 2: Ein Ritzel ist ziehbar, wenn man es entlang der Ritzelachse aus dem Eingriff herausdrehen kann
Abbildung 3: Einfluss von Messerkopfradius und Tellerradabsenkung auf die Ziehbarkei
Jetzt zum Newsletter anmelden
Registrieren Sie sich für unseren Newsletter, um die neuesten Informationen zu Antriebstechnik Software, White Papers und Weiterbildungen zu erhalten.
FVA-Workbench Features im Überblick
Sie möchten mehr über die Funktionalitäten der FVA-Workbench erfahren? Hier finden Sie einen Überblick über die aktuellen Features.